왜 노말은 월드스페이스로 변형할때 Inverse Transpose를 곱해야 할까?

유니티에서 버텍스 셰이더를 구현하다 보면 인풋으로 들어온 (오브젝트 스페이스)노말은 Inverse Transpose 행렬을 곱하여 World Space Normal로 변환하는 연산을 수행하는 걸 확인할 수 있다.

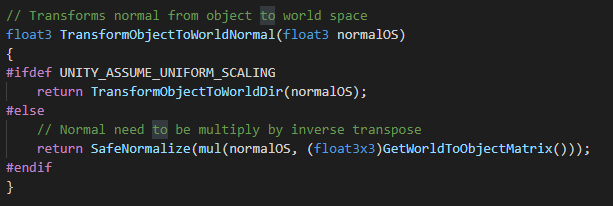
mul(normalOS, (float3x3)GetWorldToObjectMatrix()));

라인을 해석하면

1. GetWorldToObjectMatrix는 UNITY_MATRIX_I_M(Object->Model 행렬의 역행렬) 값이다.

2. mul 함수 첫번째 인자로 벡터가 들어간 경우, 두번째 인자에 들어간 행렬은 Transpose되어 곱연산이 수행된다.

즉 Object Space 노말값에 Object To World 행렬의 Inverse Transpose를 곱하는 연산을 의미한다.(주석으로도 써져 있음)

오브젝트의 노말은 월드 좌표계로 변환할때 왜 그냥 ObjectToWorld 행렬을 곱하지 않는 걸까?

이를 이해하기 위해서는 수학적인 정리가 다소 필요해 적어둔다.

---

우선 노말 좌표는 Tangent Space에 대한 이해를 필요로 한다. 오브젝트 노말은 모델의 버텍스 좌표와는 다소 다른 좌표계 상에서 정의하며, 이 좌표계를 Tangent Space라고 부른다. 이 개념을 이해했다는 가정 하에 다음 수식으로 넘어간다.

---

1

오브젝트 표면에 접하는 Tangent Space 위에 어떤 벡터 v(t)가 존재하고, 노말 벡터 v(n)에 대해 두 벡터는 직교하므로 두 벡터를 내적하면 다음과 같은 정의가 성립한다.

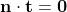
또한 위 내적 공식은 정규직교기저 정의에 의해

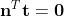
가 성립한다.

---

2

탄젠트 스페이스는 모델(=오브젝트)의 표면에 접해 있고, 따라서 탄젠트 벡터를 월드 좌표로 변환할때 Model To World Matrix 연산을 그대로 적용받는다.

---

3

탄젠트 스페이스 벡터를 월드 좌표로 변환하는 행렬을 M(B)라고 정의하면 1에서 이야기한 내적 공식은 다음과 같이 변형할 수 있다.

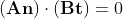
탄젠트 벡터 v(t)를 M(B)만큼 변형했을때 노말 벡터 v(n)은 M(A)만큼 변형되어야 한다는 의미.

따라서 M(A)가 우리가 구하는 답(탄젠트 공간의 노말 벡터를 월드 공간의 노말 벡터로 변형하는 행렬) 이다.

---

4

정규직교기저 정의에 의해 3의 내적 공식 역시 다음과 같이 변형 가능하다.

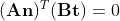
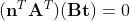
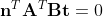
그런데 1에서

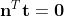
가 성립했으므로 , 두 곱연산 사이에 끼어있는 transpose(M(A))*M(B)에 대해

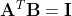
가 성립한다.

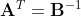
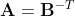
따라서 탄젠트 공간의 노말 벡터를 월드 공간의 노말 벡터로 변형하기 위해서는 Model To World Matrix의 Inverse Transpose를 곱해야 한다.

출처 StackOverflow : Why transforming normals with the transpose of the inverse of the modelview matrix?